Statistics part-2

Statistics for M.L and D.S Vol-2:

In this article, we are going to discuss some more about statistical concepts which are applied for Machine Learning(M.L) and Data Science(D.S). In the last article, we talked about some basic concepts like measures of central tendency, Inter-Quartile range, Data Matrix, Cases and Variables, some shapes of distributions. Now, we are going to cover some more concepts like Z-Score, Standard Deviation, Variance, Correlation, Regression. As i told you before, this all terminologies will help you to understand what is Data Science and Machine learning. So without wasting any time, let's move forward.

***Important note-> My coding or say python environment is the jupyter notebook, you are free to use any other environment but I'll always prefer jupyter over others. Here's the link of the first article:

Statistics for M.L and D.S Vol-1

Standard Deviation and Variance:

As we have seen in the last article, two measures of Variability i.e, Range and Inter-Quartile range. Here, we will two more measures of Variability i.e, Standard Deviation and Variance. The advantage of Variance and Standard Deviation over the other two measures is that it would take all the values of variables into account. 

Let's start with the Variance, here's the formula:

Here s^2 is the Variance, x is the value of the observation or variable, 𝑥̅ is the mean value of the variable and n is the number of observations.
Let's apply this formula to our observation:

Here we will take "Team 2" data. First, we will compute the mean,.
 import statistics
x=[10.7,10.9,17.2,30.3,23.5]
statistics.mean(x)
Now we will compute the sum of squared deviations.
a=statistics.mean(x)
l=[ ]
value=0
for values in x:
       value=values-a
       l.append(value)
       
print(sum(l))

Result:
284.528
Then we will divide this result with the total number of observations and then we get  Variance.
***Note->Larger the Variance, larger the values spread out around the mean.
But, an important disadvantage of using variance is that the metric of the variable is the metric of the variable under analysis squared. Although, we have squared the positive and negative deviations so they do not cancel out each other. In order to get rid of this problem, we will use the Standard Deviation. It is nothing but the square root of Variance. Here's the formula:

Z-Scores:

Up till now, we have seen about the variability in the distribution, like in tattoo density example, we can calculate that which data are more spread out by calculating the Range, Inter-Quartile range, Variance, Standard Deviation. But sometimes, researchers asked if a specific observation is common or exceptional. To answer this question we basically need to know how much standard deviation removed from the mean. To compute that, we will calculate Z-Score. Here's the formula:

Now we know the formula to calculate Z-Score, but what's the meaning of all this??. Let see
Look at our tattoo density example for "Team 2", we wish to calculate the Z-Score for player 2. Here are mean is 18.52 and a standard deviation is 7.54. So the Z-Score would be 10.9 minus 18.52 divided by 7.54 which is equal to 1.01. Here's the other result and the code:
x=[10.7,10.9,17.2,30.3,23.5]
mean=0

a=0
l=[ ]
value=0

for i in range(0,len(x)):
    value=value+x[i]
print(value)
mean=value/len(x)


for values in x:
    a=(values-mean)**2
    l.append(a)
standard_deviation=(sum(l)/len(x))**0.5
standard_deviation
(x[i]-mean)/standard_deviation# i = your index value

You can see, Z-Score can be both i.e positive and negative. Negative Z-Score represents value below the mean and Positive Z-Score represents value above the mean. If Z-Score is zero, that means there is no standard deviation removed from the mean, which equals the mean value because mean is the balance point of your distribution. 

But how do we get to know that Z-Score is low or high?. Well, we can find that by using a distribution curve, lemme show you that:

Here you can see 68 percent of observations fall between -1 and 1, 95 percent fall between -2 and 2, 99.7 percent fall between -3 and 3. But if the distribution is completely skewed to the right, positive values are more common because there are more extreme values to the right. And if the distribution is completely skewed to left, negative values are more common because there are more extreme values to the left.

Correlation and Regression:

Crosstabs and Scatterplots:

Most people like eating junk food. However, some people are more cautious about eating junk food, yet it might be a chance of increasing their body weight by eating junk food. Here i am going to talk about how you can find the relationship between two variable using scatter plot and contingency table in order to find that if they are correlated or not. Here's how the contingency table looks like for our two variables, body weight, and junk food consumption:

As you can see in the table, 33 individuals have a body weight of less than 50kg, 61 of 50-69 kg and so on. 27 individuals have a body weight of less than 50kg and junk food consumption is less than 50gm per week. Lemme show you the data with the percentages:

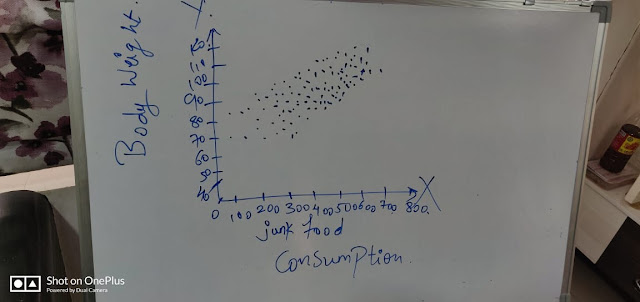
You can see that these values which define the relation of two variables are nothing but Conditional Proportions because their formation is conditional on another variable. And the values to the right are marginal proportions in we just have information of one variable. You can see from the table that the more you eat junk food, more like to weigh more, and vice versa. These shows that these two variables are correlated to each other. This phenomenon is known as Correlation. This table can be made for an ordinal or nominal variable. But for quantitative variables, Scatter plots are used. In the scatter plot, we will draw two lines, X-axis is for the independent variable which is junk food consumption and Y-axis is for the dependent variable which is for body weight. Here's how the scatter plot would look like:

Here you can easily see through the plot, the more junk food we consume, more likely to weigh more.

Pearson's r:

Well, by watching the scatter plot we can say that the two variables, i.e junk food consumption and body weight are highly correlated, but how strong is the correlation?. Well, in that case, we will use Pearson's r. Pearson's r is nothing but the measures of correlation.

As this line in the curve represents the relationship between two variables, as you can see all the points found under the clusters, this means they have a strong positive correlation. However, variables can also be correlated in different ways.

Here you can see the various kinds of relationships by these scatter plots. Scatter plots tell us whether it is a strong or weak correlation. But Pearson's r tells us how strong or weak the correlation. Pearson's r tells us the direction and exact strength of linear relationship between two quantitative variables. The value of Pearson's r ranges between -1 and 1. Here's the formula for calculating Pearson's r:

Before computing Pearson's r, you must need to plot a scatter plot in order to confirm that is there any correlation between variables or not. Let's take an example:

Here we have two variables and four cases. We need to calculate the Z-Scores of both variables and each case and find the sum of there product. We can do that either by the calculator or by following the above code. Here's the full code in order to calculate Pearson's r if you are interested to solve it by coding in python.

'''pearson r'''

x1=[50,100,200,300]

x2=[50,70,70,95]

a,b,c,d,value1,value2,prod=0

l1,l2,l3,Z_Score1,Z-Score2=[ ]

for values in x1:

    value1=value1+values

mean1=value1/len(x1)

for values in x1:

    a=(values-mean)**2

    l1.append(a)

standard_deviation1=(sum(l1)/(len(x1)-1))**0.5

standard_deviation1

for values in x2:

    value2=value2+values

mean2=value2/len(x2)

for values in x2:

    b=(values-mean2)**2

    l2.append(b)

standard_deviation2=(sum(l2)/(len(x2)-1))**0.5

standard_deviation2

for values in x1:

    c=(values-mean1)/standard_deviation1

    Z_Score1.append(c)

for values in x2:

    d=(values-mean2)/standard_deviation2

    Z_Score2.append(d)

X=sum(x*y for x,y in zip(Z_Score1,Z_Score2))

X/(len(x1)-1)

Result:
0.93
You can see how strong is the relationship between our two variables 

 Regression:

As you know now, Pearson's r tells us how strong or weak the relationship is. Here's a look:

       

    

The perfect regression line is the one which has the minimum distance of residuals. Residuals are nothing but the distance of points from the regression line as you can see in the above image. There are two kinds of residuals, the positive residuals(distance from cases above the line), and the negative residuals(distance from cases below the line). And you choose the line which has a sum of squared residuals to be smallest. Why squared residuals? Because of the positive and negative residuals cancel out each other. The sum of length os positive residuals is same as of negative residuals. But in practice, it would be hard to draw every possible line. Luckily mathematicians derived some formula in order to find the best possible line. There's one simple formula by which we can describe our regression line which is:

    

𝑦̂ is not the actual value of y, 

but it represents the predicted value of y. b is what we call the regression coefficient or the slope. It is the change in 𝑦̂ when x increases with one unit. a is what we call the intercept. It is predicted the value of y when x is zero. 

Okay, so that's all for the second part of the statistics for machine learning blog. Next article will be on probability and its distributions. So until then, happy coding!.
Here's the link of 3rd article:
Statistics part-3